Aufgabe C 2
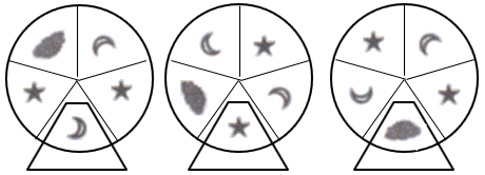
Ein Glücksspielautomat enthält drei gleiche Glücksräder, die jeweils wie dargestellt in
fünf gleich große Kreissektoren eingeteilt sind.
Bei jedem Spiel werden die Räder in Drehung versetzt und laufen unabhängig voneinander aus.
Schließlich bleiben sie so stehen, dass von jedem Rad genau ein Symbol im jeweiligen Rahmen angezeigt wird.
Ein Spieler gewinnt nur dann, wenn alle drei Räder einen Stern zeigen.
a) Weisen Sie rechnerisch nach, dass die Gewinnwahrscheinlichkeit bei einem Spiel 6,4 % beträgt.
Ein Spieler spielt 20 Spiele.
Bestimmen Sie die Wahrscheinlichkeit der folgenden Ereignisse:
A: „Der Spieler gewinnt mehr als einmal.“
B: „Der Spieler gewinnt in genau zwei Spielen und diese folgen direkt aufeinander.“
(3 VP)
b) Eine Spielerin spielt 9 Spiele.Für ein Ereignis C gilt dabei P(C)= 0,064a+9·0,0648·0,936b.
Geben Sie geeignete Werte für a und b an und beschreiben Sie das Ereignis C im Sachzusammenhang.
(2 VP)
c) Es wird vermutet, dass das mittlere Rad zu selten ein Sternsymbol zeigt. Deshalb wird die Nullhypothese „Das mittlere Rad zeigt mit einer Wahrscheinlichkeit von mindestens zwei Fünfteln ein Sternsymbol.“ getestet. Man vereinbart ein Signifikanzniveau von 3 % und einen Stichprobenumfang von 300 Drehungen.Formulieren Sie die zugehörige Entscheidungsregel.
(2,5 VP)
d) Die Glücksräder des Automaten werden durch drei neue ersetzt, die sich nicht voneinander unterscheiden. Die Glücksräder sind in mehrere gleich große Sektoren unterteilt. Jedes Glücksrad trägt in genau einem Sektor ein Sternsymbol. Man gewinnt bei 50 Spielen mit einer Wahrscheinlichkeit von mindestens 99 % höchstens einmal.Bestimmen Sie die minimale Anzahl der Sektoren pro Glücksrad.
(2,5 VP)
| Downloads |
PowerPoint